REVIEW PROBLEMS 3rd PART TOPIC 7 (a)

4.01 – 4.02 – 4.03 – 4.04 – 4.05 – 4.06 – 4.07 – 4.08 – 4.09 – 4.10 – 4.11 – 4.12 – 4.13 – 4.14 – 4.15 – 4.16 – 4.17 – 4.18 – 4.19 – 4.20 – 4.21 – 4.22 – 4.23 – 4.24 – 4.25 -

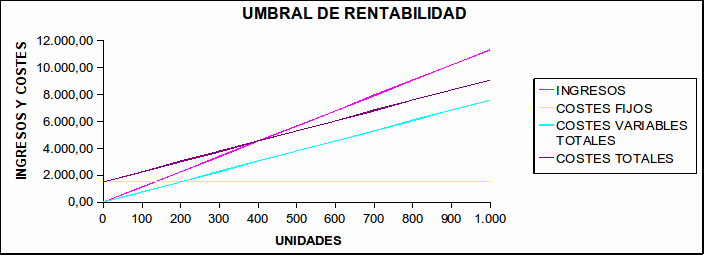
REVIEW_4.01.- The firm Landa presents the following information related to production, costs and sales revenue: OUTCOMES: BEP = 428.57; Profit = 250; P = 423 - REVIEW 4.02 - SOLUTIONS: a, b y c

1. Calculate the firm’s break-even point, explain the economic meaning of the obtained outcome and indicate in what units it’s expressed

2. Calculate the firm’s profit or loss if it produces and sells 430 units of product

3. Determinate the sale price that the firm should set ir it want its break-even point to be in 300 units of production

REVIEW_4.02.- The firm Bay’s Manufactures, Ltd acquires its raw material at an unit price of 2.85€/kg. The firm needs 22.5 tonnes. For each realised order, the firm has ones expenses of 137€ and the average time to receive the order is three days. The account department has calculated that each stored kilograme means an annual total cost of 0.1€. The firm works 320 days annually. – We want to know: OUTCOMES: Optimal order quantity = 7,851.,75; Time = 112 days; Stock level to do a new order = 210,94 - REVIEW 4.03 - SOLUTIONS: a, b y c

1. The optimal order quantity

2. How often do we need to realise the order, and

3. Which is the stock level to do a new order.

REVIEW_4.03.- According to the data of the accounts of X, Ltd: the total cost are 7,200 m.u., the fixed costs are 1,500 m.u., the sales revenue are 8,500 m.u., the firm has sold 750 units of product: OUTCOMES: BEP = 402.14; REVIEW 4.04 - SOLUTIONS: a y b

1. Calculate the break-even point, explain the economic meaning of the outcome and indicate in which units it is expressed

2. Make the chart of the total, variable and fixed costs and revenue for the following values of Q: inactivity, break-even point, sales units

REVIEW_4.04.- A firm wants to know if its productivity has increased or has decreased in the year 1998-99. In order to that, we know that during the year 1998 the firm has manufactured 7,000 products of serie A, being its unit price of 12€ and 4,500 products of serie B, being its unit price of 11.7€. To manufacture the products have worked two workers with 1,830 hours each one at 6€/hour and the firm has consumed 15,000 units of materials at 7.5€/unit. During 1999 the manufacture of the products has increased 5% and the consumption of factors has increased 2%. The number of workers and the prices have not changed: OUTCOMES: P1998 = 1.0163; P1999 = 1.0462; GPI = 1.0294 - REVIEW 4.05 - SOLUTIONS: a y b

1. Calculate the productivity of each year

2. Calculate the global productivity index

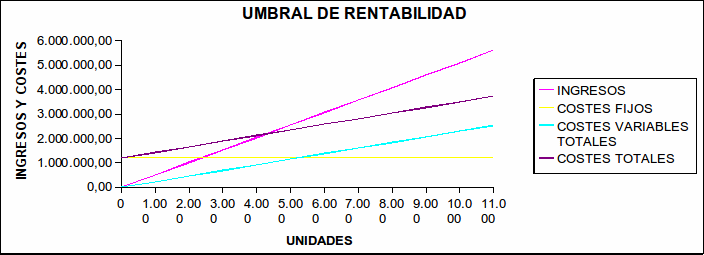
REVIEW_4.05.- A corporation wants to sell 750,000 units of a certain type of jeans. In order to that it can produce them itself or to acquire them to a textile factory. The acquisition price of the jeans to the textile factory is 7.2 €/pair. To produce these units the corporation has ones total costs of 6,325,000€, belonging 3,650,000 to variable costs. Determine: OUTCOMES: AC = 5,400,000, PC = 6,325,000 - REVIEW 4.06 - SOLUTIONS: a y b

1. The best option

2. Chart

REVIEW_4.06.- The firm RASURSA had last year a staff of 80 workers, each one of them worked 1,750 hours, reaching a production of 5,040,000 produced units of the product X. During this year it has had a staff of 68 workers, each one of them has worked 1,930 hours, being the production of this year 4,560,000 produced units of the product X: OUTCOMES: P0 = 36; P1 = 34.75 - REVIEW 4.07 - SOLUTIONS: a y b

1. Calculate the labour productivity in the periods 0 and 1

2. Analyze the evolution of the labour productivity

REVIEW_4.07.- Calculate the break-even point of a firm and the time to obtain it if its sales volume is 1,250,000€, being 13,000 the number of produced and sold units and 1,100,000€ the total costs, belonging 450,000€ to fixed costs. Express the solution in euros and in units of product. OUTCOMES: BEP = 9,750.81 p.u.; BEP = 937,540.38€; Time = 9 months - REVIEW 4.08 - SOLUTIONS 4.07

REVIEW_4.08.- The firm Furniture, Ltdl wants to know its productivity, in order to that it wants to know the productivity of both two periods (0 and 1), and the global productivity index according to the following data: OUTCOMES: P0 = 10.76; P1 = 10.94; GPI = 1.0167- REVIEW 4.09 - SOLUTIONS 4.08

REVIEW_4.09.- Determine the sales volume in which a firm that produces and sells the product X, loses 400,000 m.u. if: OUTCOME = 2,807,692.31 – REVIEW 4.10 - SOLUTION 4.09

1. The fixed costs are 2,225,000 m.u.

2. The variable costs are 35% above sales

REVIEW_4.10.- A firm has the following information about its economic activity: the operating total cost of its activity was 12,300,000€. The produced and sold units were 120,000 physical units. The firm’s Share Capital is 30,000,000€, calculate: OUTCOMES: P = 202.5; BEP = 24,478.59 - REVIEW 4.11 - SOLUTIONS: a y b

1. The sale price of the products to obtain a profitability of 40% above the firm’s share capital

2. Knowing that 25% of the total costs are fixed costs and the rest are variable costs, determine the break-even point

REVIEW_4.11.- A firm produces shelves with an industrial component. The firm can obtain this component in two ways: either manufacturing the component or acquiring it to another company that sells it at 220€ each unit. The production in the own factory would mean an annual fixed cost of 205,000€ and the unit variable cost of each component would be 50€. Each shelves needs 15 industrial components to its production. To what annual volume of production is it preferable to manufacture the industrial component or to buy it? OUTCOME = 80.39 – REVIEW 4.12 - SOLUTION 4.11

REVIEW_4.12.- A firm tries to launch to the market a new chair. It has two alternatives: a) To manufacture them, which will mean a fixed cost of 1,200,000€ and an unit variable cost of 230€/unit and b) To acquire them to a factory and to market them with its own brand, which would mean an acquisition cost of 510€/unit: OUTCOMES: a) 4,285.71; Profit = 900,000 – REVIEW 4.13 - SOLUTIONS: a, b y c

1. Explain in which case the firm is going to manufacture the chairs and when is going to buy them

1. If the firm produces 7,500 units, which will be the obtained profit or loss?

2. Make the chart

REVIEW_4.13.- A firm, that produces computers, thinks about to produce or to acquire the computer circuit board. In the market the circuit board can by acquired at 160€. It makes a research to know the production costs, with the following data: the fixed costs would be 1,200,000€ and the unit variable cost would be 80€. The firm produces and sells 17,500 computers annually. What would have to do the firm, either to produce it or to buy it? OUTCOMES: AC = 2,800,000; PC = 2,600,000 – REVIEW 4.14 - SOLUTIONS 4.13

REVIEW_4.14.- The firm “Tricycle” produces bicycles. This firm sells 15,000 bicycles annually, at a price of 180€ each one. Its unit margin (the difference between the sale price and the unit variable costs) is 50€ and its total fixed costs are 300 OUTCOMES: BEP = 6,000; Increase = 225,000 – REVIEW 4.15 - SOLUTIONS: a y b

1. Calculate the break-even point, interpreting the obtained outcome

2. In order to try to improve its profit, the firm has decided to increase the price of the bicycles in 15€. How is going to affect this decision to the firm's profit, if the number of units sold is maintained?

REVIEW_4.15.- A firm manufactures 250,000 units of the product A at 31€/unit and 120,000 units of product B at 42€/unit. The consumed factors to manufacture these products are in the following table: OUTCOMES: P1 = 138.89; P2 = 63.16; P3 = 100; P4 = 27.91- REVIEW 4.16 - SOLUTIONS 4.15

a) Calculate the productivity of each factor per product.

b) Explain its meaning and compare them

REVIEW_4.16.- The firm “Solsuero” manufactured and consumed the following products and factors for 2005 and 2006 OUTCOMES: Bº = 8.070.000, P0 = 2,45, P1 = 2,69, IPG = 1,098 – REVIEW 4.17 - SOLUTIONS: a y b

1. Calculate the profit of the year 2005 if the firm has sold all the produced units.

2. Calculate the global productivity of each year and compare them

REVIEW_ 4.17.- The sales volume in 2006 is 950,000€, being its production 19,800 units and its production costs the following:

Labour .................................................................143.400€

Raw materials.......................................................219.600€

Fixed costs............................................................312.450€

Determine the break-even point, expressing the outcome in euros and in units of product and comment the obtained outcome OUTCOMES: BEP = 10,537.94 p.u.; BEP = 505,610.36€ - SOLUTIONS 4.17

REVIEW_4.18.- The firm “M” manufactured and sold last year 30,000 tables being its total revenue 450,000€. The fixed costs were 30% above total revenue and the variable costs were 40% above this revenue. Calculate its break-even point both in physical units and in monetary units. OUTCOMES: BEP = 15,000 p.u.; BEP = 225.000 m.u. SOLUTION 4.18

REVIEW_4.19.- The firm X produced and sold 35,000 units of kitchens being its total revenue 20 million euros. The fixed cost were 700,000€. The firm's profit has been 6,000,000€. Calculate the break-even point and comment its meaning OUTCOME: BEP = 3,656.69 SOLUTION 4.19

REVIEW 4.20.- A firm produces electronic components being the production cost: C = 60Q + 150; where Q is the number of produced components and C is the production cost in euros: a) See the solution; b) See the solution; c) 62.14; d) 750; e) 10 SOLUTION 4.20

1. Which is the fixed cost and the unit variable cost of production?

2. Which is the average cost of production according to the number of produced units?

3. If the firm produces 70 units. Which is the cost per produced unit?

4. If the unit sale price is 90€. Which is the obtained profit of the firm for Q = 30 units?

5. Below which number of units of Q, the firm would have a loss being the sale price 75€/unit?

REVIEW 4.21.- A firm that is going to begin its working has to decide about the size of the technological equipment to install, being able to choose between two sizes. The production cost of the small equipment is TC_S = 75 + 4Q, and the production cost of the big one is TC_B = 300 + Q OUTCOMES: See solutions SOLUTION 4.21

1. Which is the fixed cost of each equipment?

2. Which is the unit variable cost of each equipment?

3. If it plans to produce 200 units of Q. Which is the best equipment to install?

REVIEW 4.22.- In a firm, the sales volume is 34,000 units that generates a total revenue of 600,000€ that involves a fixed cost of 80,000€ and a total variable cost of 100,000€. How many units would I have to sell if I want a profit of 120,000€? OUTCOME: 13,596.19 SOLUTION 4.22

REVIEW 4.23.- A firm produces chairs. The productive process includes the assembly and the painting. It produced last year 5,000 chairs, total cost of these chairs was 950,000 €, being 730,000 € fixed cost. This year the firm is thinking about the possibility of purchasing the chairs previously assembled. This option means to acquire the chairs at 135 € per unit. What decision must the firm make if the output for this year is 7,500 chairs?. You must calculate the production costs and the acquisition costs. OUTCOMES: Production costs = 1,060,000; Acquisition costs = 1,012,500 SOLUTION 4.23

REVIEW 4.24.- A firm made a total amount of sales of 3,200,000 € last year, being the sales price of each unit of product of 190 €. Total variable costs have been 750,000 this year and total fixed costs have been 1,500,000 € OUTCOMES: BEP = 10,311.40; PROFIT = 245,640 SOLUTION 4.24

1. Calculate the break-even point and explain its economics meaning

2. Calculate the profit or the loss that the firm would have if its sales were 12,000 physical units

REVIEW 4.25.- A firm produces two products, the model PANS and the model FREDO. The data about the output of 2008 are in the following table: OUTCOME: GP = 1.51 SOLUTION 4.25

Calculate the global productivity if the prices in 2008 were 120 € for the model PANS and 80 € for the model FREDO

SOLUTION 4.01.-

4.01 a)

Q = TFC : (P – UVC)

TC = TFC + (UVC x Q)

92,300 = 75,000 + UVC x 100

92,300 – 75,000 = 100 UVC

17,300 = 100 UVC

17,300 : 100 = UVC = 173 monetary units

TR = P x Q

34,800 = P x 100

34,800 : 100 = P = 348 monetary units

Q = 75,000 : (348 – 173) = 428.57 physical units

If we produce and sell more than 428.57 physical units we are going to obtain a profit, if we produce and sell less than this quantity we are going to obtain a loss

4.01 b)

Profit = TR – TFC – UVC x Q

Profit = P x Q – TFC – UVC x Q

Profit = 348 x 430 – 75,000 – 173 x 430

Profit = 149,640 – 75,000 – 74,390

Profit = 250 monetary units

4.01 c)

Q = TFC : (P – UVC)

300 = 75,000 : (P – 173)

300 x (P – 173) = 75,000

300 P – (300 x 173) = 75,000

300 P – 51,900 = 75,000

300 P = 75,000 + 51,900

300 P = 126,900

P = 126,900 : 300 = 423 monetary units

SOLUTION 4.02.-

4.02 a)

Q* = sqrt [(2 x D x S) : H

Q* = sqrt [(2 x 137 x 22,500) : 0.1] = 7,851.75 kgs.

4.02 b)

22,500.00 kgs. - - - - 320 days

7,851.75 kgs. - - - - x days

x = 111.67 = 112 days

4.02 c)

22,500 kgs. - - - - 320 days

x kgs. - - - - 3 days

x = 210.94 kgs.

SOLUTION 4.03.-

4.03 a)

Q = TFC : (P – UVC)

TC = TFC + (UVC x Q)

7,200 = 1,500 + UVC x 750

7,200 – 1,500 = 750 UVC

5,700 = 750 UVC

5,700 : 750 = UVC = 7.6 monetary units

TR = P x Q

8,500 = P x 750

8,500 : 750 = P = 11.33 monetary units

Q = 1,500 : (11.33 – 7.6) = 402. 14 units of product

4.03 b)

TR₀ = 11.33 x 0 = 0

TR_402,14 = 11.33 x 402-14 = 4,556.25 monetary units

TC₀ = 1,500 + (7.6 x 0) = 1,500 monetary units

TC_402,14 = 1,500 + (7.6 x 402.14) = 4,556.25 monetary units

TVC₀ = 7.6 x 0 = 0

TVC_402,14 = 7.6 x 402.14 = 3,056.26 monetary units

SOLUTION 4.04.-

4.04 a)

GP₀ = [(7,000 x 12) + (4,500 x 11.7)] : [(2 x 1,830 x 6) + (15,000 x 7.5)]

GP₀ = 136,650 : 134,460 = 1.0163

GP₁ = [(7,000 x 12 x 1.05) + (4,500 x 11.7 x 1.05)] : [(2 x 1,830 x 6 x 1.02) + (15,000 x 7.5 x 1.02)]

GP₁ = 143,482.5 : 137,149.2 = 1.0462

4.04 b)

GPI_1998-1999 = 1.0462 : 1.0163 = 1.0294

SOLUTION 4.05.-

4.05 a)

AC = P x Q

AC = 7.2 x 750,000 = 5,400,000€

PC = 6,325,000€

4.05 b)

TFC = TC – TVC

TFC = 6,325,000 – 3,650,000 = 2,675,000€

UVC = TVC : Q

UVC = 3,650,000 : 750,000 = 4.87€

Q = TFC : (P – UVC)

Q = 2,675,000 : (7.2 – 4.87) = 1,148,068.67

AC_2.000.000 = 7.2 x 2,000,000 = 14,400,000€

AC₀ = 7.2 x 0 = 0

AC_1.148.068,67 = 7.2 x 1,148,068.67 = 8,266,094.21€

PC₀ = 2,675,000 + 4.87 x 0 = 2,675,000€

PC_1.148.068,67 = 2,675,000 + 4.87 x 1,148,068.67 = 8,266,094.21€

SOLUTION 4.06.-

4.06 a)

P₀ = 5,040,000 : (80 x 1,750) = 36 produced units / hour man

P₁ = 4,560,000 : (68 x 1,930) = 34.75 produced units / hour man

4.06 b)

This firm produced 36 units of product per hour man last year and now it produces only 34.74 units, therefore the labour productivity has decreased

SOLUTION 4.07.-

TR = P x Q

125,000 = P x 13,000

125,000 : 13,000 = P = 96.15€

TC = TFC + UVC x Q

1,100,000 = 450,000 + UVC x 13,000

1,100,000 – 450,000 = 13,000 UVC

650,000 = 13,000 UVC

650,000 : 13,000 = UVC = 50€

Q = TFC : (P – UVC)

Q = 450,000 : (96.15 – 50) = 9,750.81 physical units

TR = 96.15 x 9,750.81 = 937,540.38€

13,000.00 ------------------ 12 m

9,750.81 ------------------ x m x = 9 months

SOLUTION 4.08.-

GP₀ = [(6,800 x 43) + (1,400 x 118)] : [(800 x 11) + (1,500 x 21) + (1,700 x 1.3)]

GP₀ = 457,600 : 42,510 = 10.76

GP₁ = [(6,700 x 43) + (1,480 x 118)] : [(750 x 11) + (1,510 x 21) + (1,810 x 1.3)]

GP₁ = 462,740 : 42,313 = 10.94

GPI_0-1 = 10.94 : 10.76 = 1.0167

SOLUTION 4.09.-

Profit = TR – TFC – TVC

- 400,000 = TR – 2,225,000 – 0.35 TR

2,225,000 – 400,000 = TR – 0.35 TR

1,825,000 = 0.65 TR

1,825,000 : 0.65 = TR = 2,807,692.31€

SOLUTION 4.10.-

4.10 a)

Profit = P x Q – TC

30,000,000 x 0.4 = P x 120,000 – 12,300,000

12,000,000 = 120,000 P – 12,300,000

12,000,000 + 12,300,000 = 120,000 P

24,300,000 = 120,000 P

24,300,000 : 120,000 = P = 202.5€

4.10 b)

TFC = 12,300,000 x 0.25 = 3,075,000€

TVC = 12,300,000 x 0.75 = 9,225,000€

UVC = 9,225,000 : 120,000 = 76.88€

Q = 3,075,000 : (202.5 – 76.88) = 24,478.59 physical units

SOLUTION 4.11.-

Q = TFC : (P – UVC) = 205,000 : [(220 x 15) – (50 x 15)]

Q = 80.39 shelves

SOLUTION 4.12.-

4.12 a)

Q = TFC : (P – UVC)

Q = 1,200,000 : (510 – 230) = 4,285.71 physical units

4.12 b)

AC = P x Q = 510 x 7,500 = 3,825,000€

PC = TFC + UVC x Q = 1,200,000 + (230 x 7,500) = 2,925,000€

Profit = 3,825,000 – 2,925,000 = 900,000€

4.12 c)

AC_8.000 = 510 x 8,000 = 4,080,000€

AC₀ = 510 x 0 = 0

AC_4.285,71 = 510 x 4,285.71 = 2,185,712.1€

PC₀ = 1,200,000 + 230 x 0 = 1,200,000€

PC_4.285,71 = 1,200,000 + 230 x 4,285.71 = 2,185,712.1€

SOLUTION 4.13.-

AC = 160 x 17,500 = 2,800,000€

PC = 1,200,000 + (80 x 17,500) = 2,600,000€

SOLUTION 4.14.-

4.14 a)

Q = 300,000 : 50 = 6,000 bicycles

4.14 b)

UVC = 180 – 50 = 130€

Profit = P x Q – TFC – UVC x Q

Profit before = (180 x 15,000) – 300,000 – (130 x 15,000) = 450,000€

Profit after = (195 x 15,000) – 300,000 – (130 x 150,000) = 675,000€

Increase = 225.000€

SOLUTION 4.15.-

Labour productivity A = 250,000 : 1,800 = 138.89 units of product / hour man

Labour productivity B = 120,000 : 1,900 = 63.16 units of product / hour man

Machine productivity A = 250,000 : 2,500 = 100 units of product / hour machine

Machina productivity B = 120,000 : 4,300 = 27.91 units of product / hour machine

SOLUTION 4.16.-

4.16 a)

Profit = TR – TC

Profit = [(13,000 x 420) + (16,000 x 510)] – [(2,100 x 2,200) + (30,000 x 31)]

Profit = 13,620,000 – 5,550,000 = 8,070,000€

4.16 b)

P₂₀₀₅ = [(13,000 x 420) + (16,000 x 510)] : [(2,100 x 2,200) + (30,000 x 31)] = 2.45

P₂₀₀₆ = [(11,000 x 420) + (18,000 x 510)] : [(1,900 x 2,200) + (30,400 x 31)] = 2.69

GPI_2005-2006 = 2.69 : 2.45 = 1.098

The global productivity has increased 9.8%

SOLUTION 4.17.-

UVC = TVC : Q

UVC = (143,400 + 219,600) : 19,800 = 18.33€

TR = P x Q

950,000 = P x 19,800

950,000 : 19,800 = P = 47.98€

Q = TFC : (P – UVC) = 312,450 : (47.98 – 18.33) = 10,537.94 physical units

TR = 47.98 x 10,537.94 = 505,610.36€

SOLUTION 4.18.-

TFC = 450,000 x 0.3 = 135,000

TVC = 450,000 x 0.4 = 180,000

UVC = 180,000 : 30,000 = 6

P = 450,000 : 30,000 = 15

Q = 135,000 : (15 – 6) = 15,000

TR = P x Q = 15 x 15,000 = 225,000

SOLUTION 4.19.-

Profit = TR – TFC – UVC x Q

6,000,000 = 20,000,000 – 700,000 – UVC x 35,000

35,000 UVC = 20,000,000 – 700,000 – 6,000,000

35,000 UVC = 13,300,000

UVC = 13,300,000 : 35,000 = 380

TR = P x Q

20,000,000 = P x 35,000

P = 20,000,000 : 35,000 = 571.43

Q = TFC : (P – UVC) = 700,000 : (571.43 – 380) = 3,656.69 kitchens

If we produce and sell more than 3,656.69 kitchens we has a profit, otherwise we have a loss

SOLUTION 4.20.-

a.-

TFC = 150 UVC = 60

b.-

Average cost = TC : Q = (60Q + 150) : Q = 60 + (150 : Q)

c.-

Average cost₇₀ = (60 x 70 + 150) : 70 = 62.14

d.-

Profit = P x Q – TFC – UVC x Q

Profit = 90 x 30 – 150 – 60 x 30 = 2,700 – 150 – 1,800 = 750

e.-

Q = TFC : (P – UVC) = 150 : (75 – 60) = 10

SOLUTION 4.21.-

a.-

TFCs = 75; TFCb = 300

b.-

UVCs = 4; UVCb = 1

c.-

TCs = 75 + 4 x 200 = 875

TCb = 300 + 200 = 500

SOLUTION 4.22.-

TR = P x Q

600,000 = P x 34,000

P = 600,000 : 34,000 = 17.65

UVC = TVC : Q = 100,000 : 34,000 = 2.94

Profit = P x Q – TFC – UVC x Q

120,000 = 17.65 Q – 80,000 – 2.94 Q

120,000 + 80,000 = 17.65 Q – 2.94 Q

200,000 = 14.71 Q

Q = 200,000 : 14.71 = 13,596.19 p.u.

SOLUTION 4.23.-

TC = TFC + UVC x Q

950,000 = 730,000 + UVC x 5,000

950,000 – 730,000 = UVC x 5,000

220,000 = UVC x 5,000

220,000 : 5,000 = UVC = 44 €

Production costs = TFC + UVC x Q

Production costs = 730,000 + 44 x 7,500 = 1,060,000 €

Acquisition costs = P x Q

Acquisition costs = 135 x 7,500 = 1,012,500 €

The firm would buy the chairs previously assembled because of it is cheaper

SOLUTION 4.24.-

TR = P x Q

3,200,000 = 190 x Q

3,200,000 : 190 = Q = 16,842.11 physical units

TVC = UVC x Q

750,000 = UVC x 16,842.11

750,000 : 16,842.11 = UVC = 44.53 €

Q = TFC : (P – UVC)

Q = 1,500,000 : (190 – 44.53) = 10,311.40 physical units

If we produce and sell more than 10,311.40 physical units we have a profit, otherwise we have a loss

PROFIT = P x Q – TFC – UVC x Q

PROFIT = 190 x 12,000 – 1,500,000 – 44.53 x 12,000 = 245,640 €

SOLUTION 4.25.-

GP = [(P₁ x Q₁) + (P₂ x Q₂) + . . . + (P_n x Q_n)] : [(f₁ x F₁) + (f₂ x F₂) + . . . + (f_n x F_n)]

GP = [(860 x 120) + (780 x 80)] : (50,000 + 60,000) = 1.51